六角形のタイルが敷き詰められた都市で、そのタイルの辺に沿って移動するときの距離(以下、つくば距離と呼ぶ)について考える。
「マンハッタン距離」ではなく「つくば距離」は定義できるかな? https://t.co/y6MRAct28J
— AXION (@AXION_CAVOK) December 9, 2023
・直感的な答え
六角形のタイルを敷き詰めたとき、どこに向かってもその経路はジグザグになるが、方向によってその距離は異なる。1辺の長さを \(1\) とすると、タイルの辺に平行な方向(下図の赤線)に進むときは、辺に沿って \(4\) 進むと原点からは \(3\) 離れる。一方で、辺に垂直な方向(青線)に進むときは、 辺に沿って \(2\) 進むと原点から \(\sqrt3\) 離れることになる。つまり、同じつくば距離を進んでも、向きが30度違うと原点からのユークリッド距離は \(2/\sqrt3\) 倍だけ異なるわけで、そのような図形(”等つくば距離線”の形)とは、正六角形である。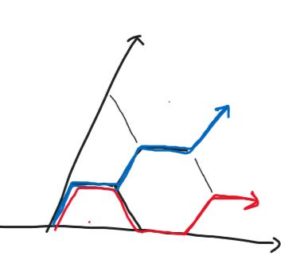
・もう少し真面目に考えてみる
直感的に正六角形でありそうだ、ということはわかったが、本当にそうだろうか?
まずはタイルに沿った座標系を考える必要があるだろう。図のように60度の角度で交わる軸 \(\xi, \eta\) を考え、それぞれの方向の単位ベクトルを \(\boldsymbol i, \boldsymbol j\) としよう。さらに、\(\boldsymbol j\) と60度をなすベクトルを \(\boldsymbol k\) として、それら逆向きのベクトルを、上にバーをつけて表そう。
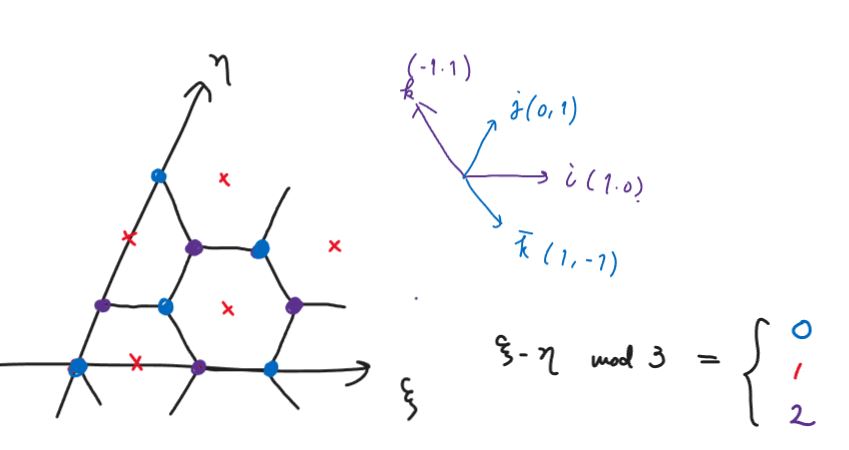
平面上の格子点は、剰余$$\xi-\eta \mod 3$$によって分類することができる。つまり
- 剰余が0(青) →\(\boldsymbol j, \bar{\boldsymbol i}, \bar{\boldsymbol k}\) 方向に進める
- 剰余が1(赤) →頂点ではない
- 剰余が2(紫) →\(\boldsymbol i, \boldsymbol k, \bar{\boldsymbol j}\) 方向に進める
ということである。
いま、タイルのパターンは120度回転対称で、また \(\xi, \eta\) 軸に対して鏡対称なので、右上の60度の領域についてだけ考えれば良い。ゆえに、移動する方向も \(\boldsymbol i, \boldsymbol j, \boldsymbol k, \bar{\boldsymbol k}\) だけを考えればよい。
さて、原点から辺に沿って \(2n\) 回移動して到達可能な点の集合を考える。隣り合う頂点とは必ず剰余の値が違うので、どんな経路を通っても青と紫の点を交互に辿ることになる。したがって半分の \(n\) 回は青の点から、もう半分の \(n\) 回は紫の点から移動することになる。紫の点から \(\boldsymbol i\) 方向に進むことを選んだ回数を \(p\) とおき、青の点から \(\boldsymbol j\) 方向に進むことを選んだ回数を \(q\) とおくと、最終的に到達する点の位置ベクトルは$$p\boldsymbol i+q\boldsymbol j+(n-p) \boldsymbol k+(n-q)\bar{\boldsymbol k}$$
である。ここに、$$\begin{eqnarray*}
\boldsymbol i &=& (1, 0)\\
\boldsymbol j &=& (0, 1)\\
\boldsymbol k &=& (-1, 1)
\end{eqnarray*}$$
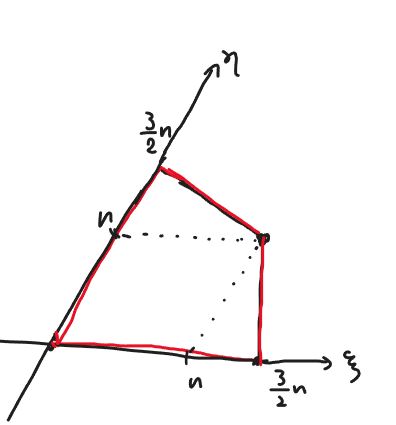
であるから、これを用いて到達点の成分を書き下すと$$(2p-q, 2q-p)$$となる。\(0\leq p\leq n, 0 \leq q \leq n\) かつ \(\xi\geq 0, \eta\geq 0\) の範囲でこれが取りうる範囲を \(\xi \mathrm{-} \eta\) 平面上に図示すると、下図の赤で囲んだ四辺形の内側の領域となる。領域全体はつくば距離が\(0\) 以上 \(2n\) 以下の点の集合なので、つくば距離が \(2n\) に等しくなるのは境界のうち軸と共通でない部分となる。これは正六角形の1/6だから、確かに等距離線の形は正六角形になることがわかる。
・信用できないのでプログラムで確かめる
幅優先探索で実際に好きなつくば距離だけ離れた点の集合を列挙するプログラムを書いた。gistに置いてあるので気になる人はどうぞ。
距離が小さいうちは距離が奇数だと若干非対称になり正六角形にはならないが、距離が大きくなると正六角形に近づく。以下に距離が \(5, 6, 31\) の例を示す。
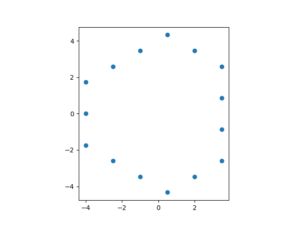
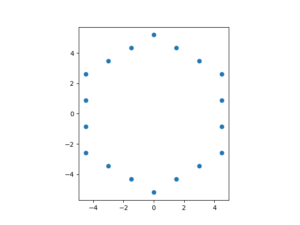
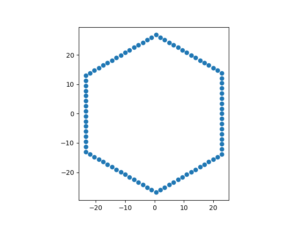
ユークリッド距離、マンハッタン距離との比較も示す。冒頭で述べた通り、\(x\)軸との交点は \(3/4\), \(y\)軸との交点は \(\sqrt3/2\) である。
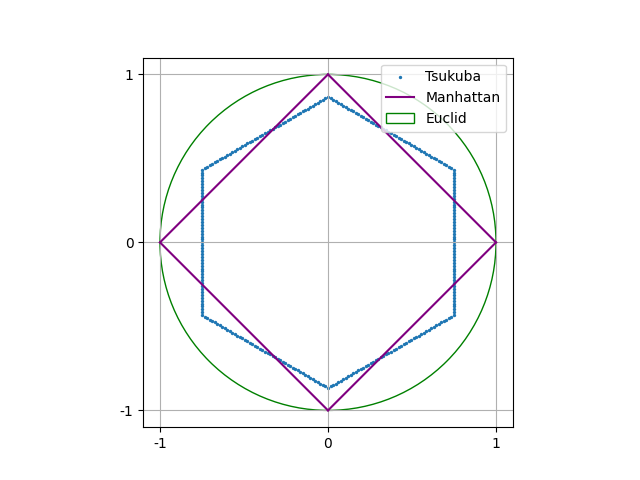
実際にこんな道路があったらめちゃくちゃ通りにくいだろうと思う。