試験期間おなじみの逃避記事。
・前提
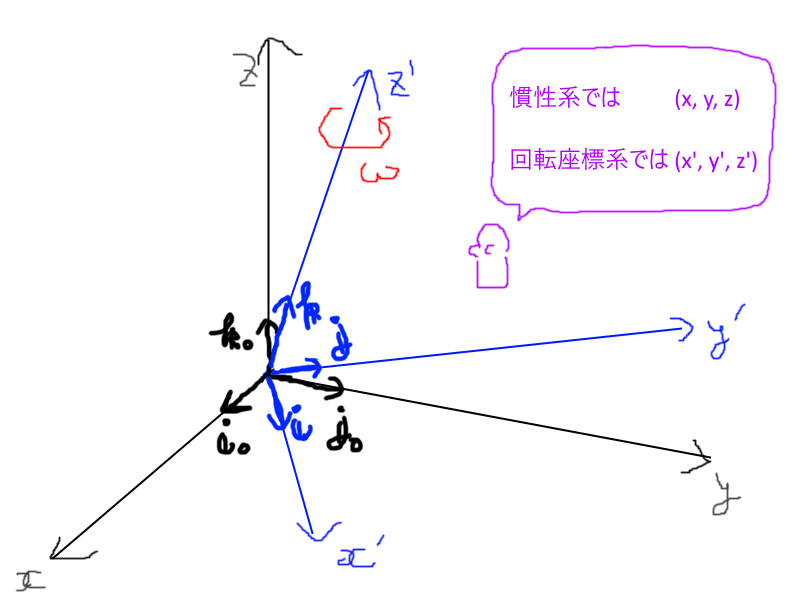
慣性座標系\(O-xyz\)系と、角速度\(\boldsymbol \omega\)で回る回転座標系\(O-x^\prime y^\prime z^\prime\)系が、原点を共有しているような状況を考える。なお、図では回転座標系が\(z^\prime\)軸周りに回転しているが、回転座標系の回転軸は別に座標軸に一致していなくても構わない。
慣性座標系の基底を\(\mathscr W=\{\boldsymbol i_0,\boldsymbol j_0,\boldsymbol k_0\}\)とし、回転座標系の基底を\(\mathscr V=\{\boldsymbol i,\boldsymbol j,\boldsymbol k\}\)とする。
慣性座標系から物体を見た座標ベクトルを$$\boldsymbol R=\left[\begin{array}{cc}x\\y\\z\end{array}\right]$$とし、回転座標系から物体を見た座標ベクトルを$$\boldsymbol r=\left[\begin{array}{cc}x^\prime\\y^\prime\\z^\prime\end{array}\right]$$とする。
・位置に関する関係式
慣性座標系と回転座標系で、見かけの座標は異なるが、実体の位置は同じである。つまり
$$x\boldsymbol i_0+y\boldsymbol j_0+z\boldsymbol k_0 = x^\prime\boldsymbol i+y^\prime\boldsymbol j+z^\prime\boldsymbol k$$
である。基底と座標ベクトルを使えば、
$$\mathscr W\boldsymbol R=\mathscr V\boldsymbol r\quad\cdots(1)$$
と書ける。
・速度に関する関係式
先の(1)式の両辺を微分する。
$$\begin{eqnarray}\frac{\mathrm d}{\mathrm dt}(\mathscr W\boldsymbol R)&=&\frac{\mathrm d}{\mathrm dt}(\mathscr V\boldsymbol r)\\
\Leftrightarrow\frac{\mathrm d\mathscr W}{\mathrm dt}\boldsymbol R+\mathscr W\frac{\mathrm d\boldsymbol R}{\mathrm dt}&=&\frac{\mathrm d\mathscr V}{\mathrm dt}\boldsymbol r+\mathscr V\frac{\mathrm d\boldsymbol r}{\mathrm dt}\quad\cdots(2)
\end{eqnarray}$$
ここで、慣性座標系の基底である\(\mathscr W\)は時間変化しないので、(2)式の左辺の第一項は0である。一方で、右辺第一項については、回転座標系の基底\(\mathscr V\)は角速度\(\boldsymbol \omega\)で回転しているので、この影響を考えなくてはならない。
角速度ベクトルの定義を考えれば、
$$\begin{eqnarray}\frac{\mathrm d\boldsymbol i}{\mathrm dt}&=&\boldsymbol \omega \times\boldsymbol i\\
\frac{\mathrm d\boldsymbol j}{\mathrm dt}&=&\boldsymbol \omega \times\boldsymbol j\\
\frac{\mathrm d\boldsymbol k}{\mathrm dt}&=&\boldsymbol \omega \times\boldsymbol k\end{eqnarray}$$
であるので、$$\frac{\mathrm d\mathscr V}{\mathrm dt}\boldsymbol r=\boldsymbol \omega\times(\mathscr V\boldsymbol r)$$
が成り立つ。これより$$\mathscr W\frac{\mathrm d\boldsymbol R}{\mathrm dt}=\boldsymbol \omega\times(\mathscr V\boldsymbol r)+\mathscr V\frac{\mathrm d\boldsymbol r}{\mathrm dt}\quad\cdots(3)$$となる。
(3)式の左辺は慣性座標系から見た物体の速度\(\boldsymbol V\)である。一方で、右辺第一項は回転座標系の回転によって生じる速度であり、右辺第二項が回転座標系から見た物体の速度\(\boldsymbol v\)となる。ここまでは直感的にもわかりやすい。
・加速度に関する関係式
(3)式の両辺をさらに微分する。
$$\begin{eqnarray}
\frac{\mathrm d}{\mathrm dt}\left(\mathscr W\frac{\mathrm d\boldsymbol R}{\mathrm dt}\right)&=&\frac{\mathrm d}{\mathrm dt}\left(\boldsymbol \omega\times(\mathscr V\boldsymbol r)+\mathscr V\frac{\mathrm d\boldsymbol r}{\mathrm dt}\right)\\
\Leftrightarrow\quad\quad\mathscr W\frac{\mathrm d^2\boldsymbol R}{\mathrm dt^2}&=&\frac{\mathrm d\boldsymbol \omega}{\mathrm dt}\times(\mathscr V\boldsymbol r)+\boldsymbol \omega\times\frac{\mathrm d}{\mathrm dt}(\mathscr V\boldsymbol r)+\frac{\mathrm d\mathscr V}{\mathrm dt}\frac{\mathrm d\boldsymbol r}{\mathrm dt}+\mathscr V\frac{\mathrm d^2\boldsymbol r}{\mathrm dt^2}\\
\Leftrightarrow\quad\quad\mathscr W\frac{\mathrm d^2\boldsymbol R}{\mathrm dt^2}&=&\frac{\mathrm d\boldsymbol \omega}{\mathrm dt}\times(\mathscr V\boldsymbol r)+\boldsymbol \omega\times\left(\boldsymbol \omega\times(\mathscr V\boldsymbol r)+\mathscr V\frac{\mathrm d\boldsymbol r}{\mathrm dt}\right)+\boldsymbol\omega\times\left(\mathscr V\frac{\mathrm d\boldsymbol r}{\mathrm dt}\right)+\mathscr V\frac{\mathrm d^2\boldsymbol r}{\mathrm dt^2}\\
\Leftrightarrow\quad\quad\mathscr W\frac{\mathrm d^2\boldsymbol R}{\mathrm dt^2}&=&\frac{\mathrm d\boldsymbol \omega}{\mathrm dt}\times(\mathscr V\boldsymbol r)+\boldsymbol \omega\times(\boldsymbol \omega\times(\mathscr V\boldsymbol r))+2\boldsymbol\omega\times\left(\mathscr V\frac{\mathrm d\boldsymbol r}{\mathrm dt}\right)+\mathscr V\frac{\mathrm d^2\boldsymbol r}{\mathrm dt^2}\\
\end{eqnarray}$$
左辺は1項しかないのに対し右辺は項が4つもある。もうなにがなんだかわからないが、さらに両辺に物体の質量\(m\)をかけてみよう。
$$\mathscr Wm\frac{\mathrm d^2\boldsymbol R}{\mathrm dt^2}=m\frac{\mathrm d\boldsymbol \omega}{\mathrm dt}\times(\mathscr V\boldsymbol r)+m\boldsymbol \omega\times(\boldsymbol \omega\times(\mathscr V\boldsymbol r))+2m\boldsymbol\omega\times\left(\mathscr V\frac{\mathrm d\boldsymbol r}{\mathrm dt}\right)+\mathscr Vm\frac{\mathrm d^2\boldsymbol r}{\mathrm dt^2}$$
さらに回転座標系視点で考えるためにゴチャゴチャと移項する。
$$\mathscr Vm\frac{\mathrm d^2\boldsymbol r}{\mathrm dt^2}=\mathscr Wm\frac{\mathrm d^2\boldsymbol R}{\mathrm dt^2}-m\frac{\mathrm d\boldsymbol \omega}{\mathrm dt}\times(\mathscr V\boldsymbol r)-m\boldsymbol \omega\times(\boldsymbol \omega\times(\mathscr V\boldsymbol r))-2m\boldsymbol\omega\times\left(\mathscr V\frac{\mathrm d\boldsymbol r}{\mathrm dt}\right)$$
まず左辺の\(m\frac{\mathrm d^2\boldsymbol r}{\mathrm dt^2}\)は回転座標系で観測された物体にかかる力\(\boldsymbol F\)である。一方右辺第一項の\(m\frac{\mathrm d^2\boldsymbol R}{\mathrm dt^2}\)は慣性座標系で観測された力であることから、外力\(\boldsymbol f\)を表している。つまり
$$\mathscr V\boldsymbol F=\mathscr W\boldsymbol f-m\frac{\mathrm d\boldsymbol \omega}{\mathrm dt}\times(\mathscr V\boldsymbol r)-m\boldsymbol \omega\times(\boldsymbol \omega\times(\mathscr V\boldsymbol r))-2m\boldsymbol\omega\times\left(\mathscr V\frac{\mathrm d\boldsymbol r}{\mathrm dt}\right)\quad\cdots(4)$$
であり、回転座標系で物体にかかっているように見える力\(\boldsymbol F\)のうち、実際にかかっているのは右辺第一項の\(\boldsymbol f\)だけで、残りは見かけの力、すなわち慣性力ということになる。
(4)式右辺第二項は回転座標系の角加速度\(\frac{\mathrm d\boldsymbol \omega}{\mathrm dt}\)によるもので、特に名前がなく、等角速度の系を扱うときは無視されてしまう可哀そうな項である。
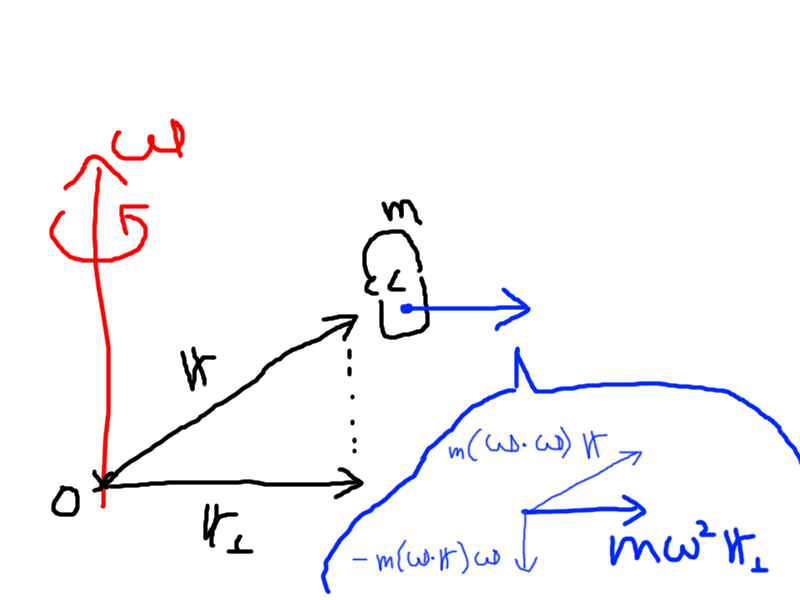
(4)式右辺第三項は遠心力$$-m\boldsymbol \omega\times(\boldsymbol \omega\times(\mathscr V\boldsymbol r))$$である。大きさは\(mr_\perp\omega^2\)であり、向きは\(\boldsymbol\omega\)に垂直で\(\boldsymbol r_\perp\)に平行である。
これはベクトル三重積の公式を使うと理解できる。$$-m\boldsymbol \omega\times(\boldsymbol \omega\times(\mathscr V\boldsymbol r))=m(\boldsymbol \omega\cdot\boldsymbol \omega)\mathscr V\boldsymbol r-m(\boldsymbol \omega\cdot(\mathscr V\boldsymbol r))\boldsymbol \omega\quad\cdots(5)$$
(5)式右辺各項の\(\boldsymbol\omega\)に平行な成分は大きさが同じ\(mr_{//}\omega^2\)であるので打ち消しあい、\(\boldsymbol r_\perp\)に平行な成分のみが残る。
そして(4)式右辺第四項がお待ちかねコリオリ力$$-2m\boldsymbol\omega\times\left(\mathscr V\frac{\mathrm d\boldsymbol r}{\mathrm dt}\right)$$である。大きさは\(2m\omega v_\perp\)、向きは\(\boldsymbol\omega\)および\(\boldsymbol v_\perp\)に垂直である。下図でいうと画面に対して垂直手前方向に力がかかることになる。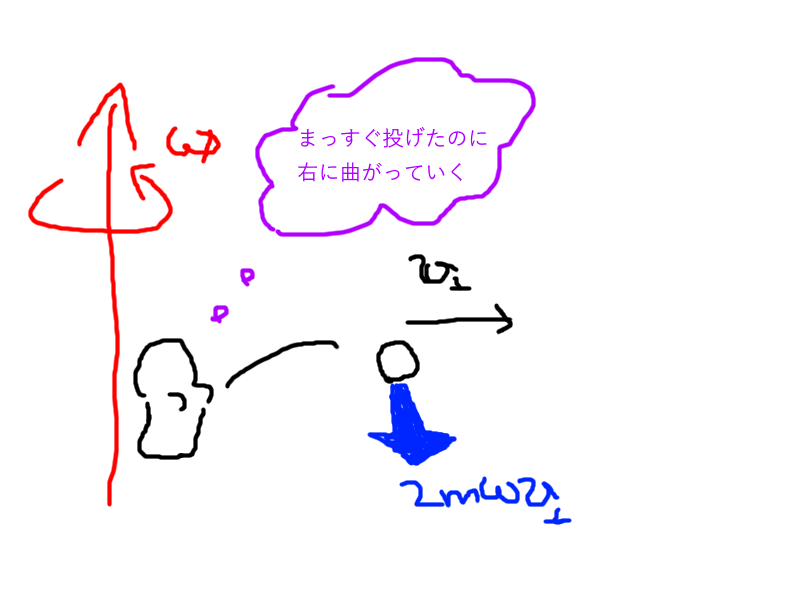
基底を明示的にすると座標系に依る視点の違いをすんなり理解できるなと思ってやってみたが、見た目がよくないのが難点である。この形なら正規直交基底でなくても成り立つはず。