円をグルグルして図形を描いてみよう。
・こういうやつ
Twitterでこんな感じのの動画を見たことがあるだろうか。
円が連なって、まるでロボットアームのように図を描き出していく。今回はこれを作っていく。
・原理
画面を複素平面に見立てると、画面上の点はある1つの複素数 \(z\) と対応させることができる。これを時刻 \(t\) によって変化する実数変数複素関数 \(z=f[t]\) とみなすことで、離散フーリエ変換することができる。フーリエ変換についてはこの記事で触れているので参考にされたい。
変換の結果得られたものを \(F[k]\) とすると、フーリエ逆変換の公式より元の関数は次のように表せる。$$f[t]=\sum^{N-1}_{k=0} F[k]e^{i\frac{2\pi k}{N}t}$$
\(\displaystyle e^{i\frac{2\pi k}{N}t}\) は、角速度\(\displaystyle \frac{2\pi k}{N}\) で単位円上を周回する点とみなすことができる。そこに\(F[k]\)を掛けるということは、単位円の半径を \(r_k=|F[k]|\) 倍し、初期位相を\(\phi_k=\arg F[k]\)だけずらすことと同等であるから、上の式は
$$f[t]=\sum^{N-1}_{k=0} r_ke^{i\left(\frac{2\pi k}{N}t+\phi_k\right)}$$と表せる。
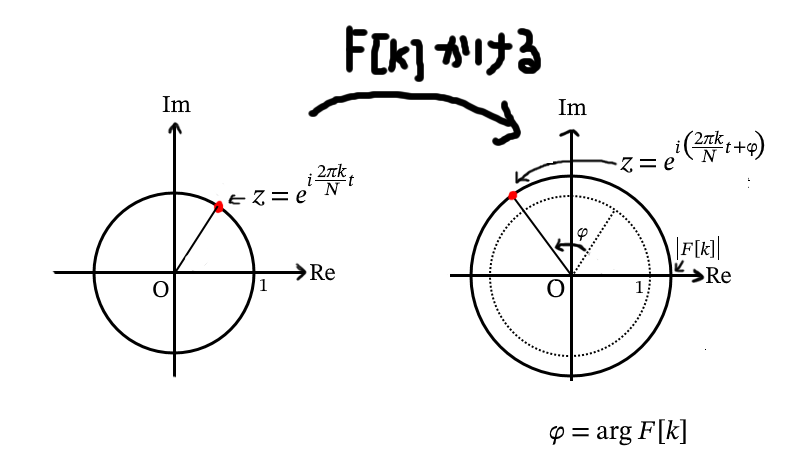
また、総和をとるということは、複素平面上において、\(k\)番目の円の上を周回する点を中心として\(k+1\)番目の円を描き、さらにその円の上を周回する点を中心として\(k+2\)番目の円を描き...ということを行うのと同等であるから、円を重ねることでフーリエ逆変換ができ、元の関数が表現されるというわけである。
・図を2個描きたい
さて、円の重ね合わせで図を描けることがわかったので、冒頭に示した動画のように2つの図を描く方法を考えよう。
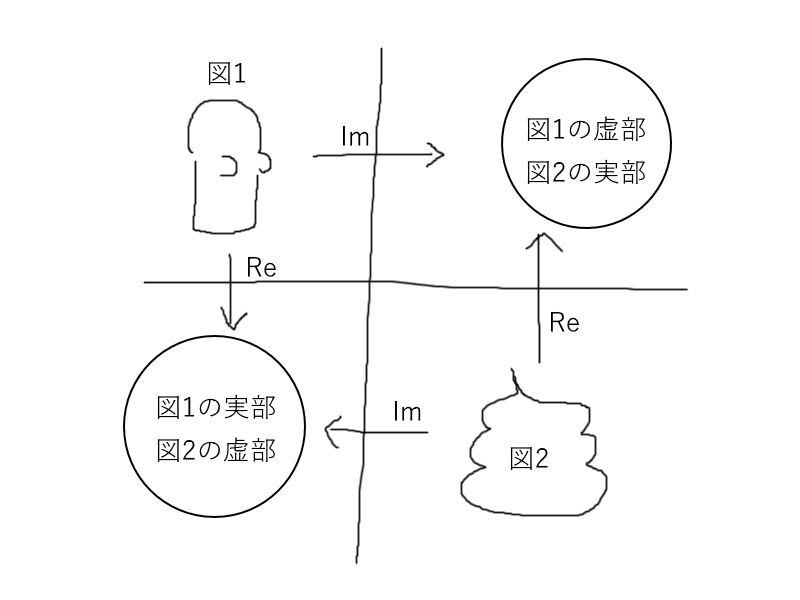
右上は1つ目の図の虚部と2つ目の図の実部を担当し、左下は1つ目の図の実部と2つ目の図の虚部を担当していることになるので、2つの図の実部か虚部を交換してやってから離散フーリエ変換すればよいことになる。
・実装
ソースコードのほとんどが描画処理の文なのでコードをすべて載せることはしないが、中心的な部分について少し言及しておく。
上の説明では円を表すうえで\(e^{i\theta}\)という形を使ったが、実際に実装するとなると実部・虚部を\(x\)・\(y\)に対応させる必要があるので、この形では不便である。そこで、オイラーの等式\(e^{i\theta}=\cos \theta+i\sin \theta\)を使うと実部・虚部を別々に処理できるので便利である。下にjavaでの実装(の一部)を載せておく。
for (int k=0; k<N; k++) {
Complex coef1 = spectrum[0][k]; //F[k]の値
Complex coef2 = spectrum[1][k];
float th = 2 * PI * k * t / N;
float th1 = th + coef1.Phi(); //位相をずらす
float th2 = th + coef2.Phi();
float amp1 = coef1.Abs(); //振幅(円の半径)
float amp2 = coef2.Abs();
x1 += amp1 * cos(th1); //実部
y1 += amp2 * sin(th2); //虚部
x2 += amp2 * cos(th2);
y2 += amp1 * sin(th1);
}
というわけで円をぐるぐるして図を描くことができた(?)。フーリエ変換は楽しい。